One of the most important concepts in crowd safety is queueing theory.
Q: What is Queueing Theory ?
A: The primary tool for studying the problem of congestion is known as Queueing Theory. Any system in which arrivals place a demand upon a finite capacity, a limited space or limited resources may be termed a Queueing System. Queueing Theory is a branch of statistics which deals with arrival times of people (or transport) and service rates (time taken for change, or buying something, tickets, gates, etc).
Q: What are some of the applications of queueing theory?
A: Queueing theory is useful in crowd safety management, turnstile design, entry and exit systems, concession planning and crowd flow assessment, venue ticket sales, queueing race design and transport loading (to and from a venue), density and emergency egress analysis, traffic control and planning, determining the sequence of computer operations, predicting computer performance, telecommunications, health services (eg. control of hospital bed assignments), airport traffic, airline ticket sales, the mining industry, layout of manufacturing systems, capacity planning for busses and trains, dwell time analysis at stations and many more logistic problems that can effect a venue. It is even useful in determining when to remove a goalie in a hockey game!
There are many books written about "Queueing Theory" and we run workshops on the basics of modelling queues, congestion and systems analysis.
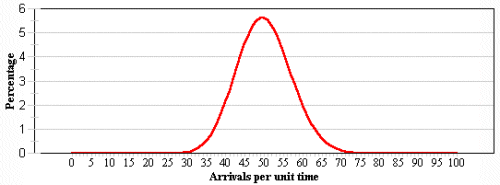
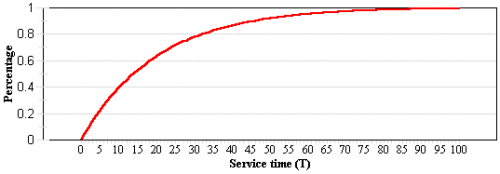
The single-channel queueing model with poisson arrivals and exponential service times.
The basic principles are that queues have an arrival rate, a service rate, and a discipline. The accepted method of defining a queue uses the following symbols.
λ = Expected number of arrivals per time period (mean arrival rate)
μ = Expected number of services possible per time period (mean service rate)
Using the following assumptions:-
- The queue has a single channel
- The pattern of arrivals follow a Poisson probability distribution
- The service times follow an exponential probability distribution
- The queue discipline is first come, first served
Formulae for calculating the following:
Probability that there is no-one in the queue (P0)
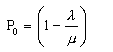
Probability of N people in the system (PN)
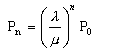
The average number of people in the queue (Lq)

The average number of people in the system (L)
![]()
The average time a person spends waiting in the queue (Wq)

The average time a person spends in the system (W)
![]()
The probability that a person has to wait in the queue (Pw)
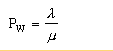
All of the above calculations can be integrated into a spreadsheet model to provide the user with the critical information about queueing duration, size, length of wait. etc.
