5 Introduction
We have defined the basic criteria necessary for a simulation of large crowds. In this chapter we shall outline the parameters, assumptions and characteristics of the Legion simulation system, which is the central topic of this thesis.
The Legion simulation consists of independent problem-solving entities which obey the OMCA rules. These entities move around a two dimensional computer-generated landscape and read and react to changes in that environment. These reactions include responses to the behaviour of other entities.
Like the ants in a colony, Legion entities are automata with limited intelligence. This fulfils one of our safety criteria for, if we were to make the entities too smart, they would never endanger themselves. The simulation is designed to discover the situations in which people can cause themselves harm and, by design, reduce or eliminate the associated risks. We discuss the reasons for the assumptions behind the methodology used in the simulation.
5.1 Choosing the simulation parameters
We need to represent the entity and the geometry on an appropriate scale. We also need to determine the scope and scale of the models we wish to build, the number of entities in a typical model, and the features that we wish to measure. We need to define the crowd parameters and how they relate to the issues of safety.
The parameters of the crowd dynamic, used in the simulation include the following:
- Entity Sizes Dimensions of height, breadth and depth for entities.
- Space The space entities occupy when moving, standing or changing route. That is, a plan of the building.
- Time An appropriate choice of time-slicing (dividing the time frame) to allow the simulation to be viewed in real-time.
- Movement The distance that entities advance for each unit of time.
- Decisions The algorithm for choosing where to go next.
5.2 Modelling people
People come in all shapes and all sizes and large breadth does not imply a large depth. From Bodyspace [38] we can see those individual dimensions, chest depth, shoulder breadth etc., form normal distribution curves. We also note that an individual who is tall may not necessarily be faster than a shorter person.
We need to provide a clear and anthropomorphically correct graphical representation for our simulated humans. We also need to consider their movement in steps per frame. Furthermore there is a need to consider the computational overheads in both processing and display of the entities. There are two options for our choice of entity size in the simulation.
- Give each entity its own size From the distribution histogram.
- Give each entity size the same size Taking the average, or largest size from the distribution histogram
5.2.1 Choosing the 95th percentile
If we can prove that the environment we wish to simulate works with a capacity crowd in the 95th percentile range, then we are testing the upper limits of the environment. We should not forget that there are situations where the crowd could consist of people who are all larger than this - a rugby club reunion for example, or the local weight watcher’s outing to Bognor Regis.
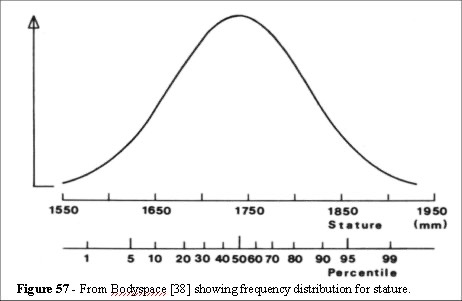
Figure 57 shows that the choice of the 95th percentile covers the mean population dimensions (the distribution curve is valid for breadth and depth). To facilitate the exceptional circumstances of an abnormally large framed population we shall provide scaling within the system.
However, we are considering the crowd dynamics and the evidence presented by Kendik et al. [22, 32-34, 38, 57-62, 79-87] indicates that entity sizes are distributed normally around the mean value (Figure 57).
Although there may be exceptional circumstances where members of the population are all above the 95th percentile in both breadth and depth, we are considering entity density. Our primary concern is how many people per square metre we can allow while maintaining a safe environment.
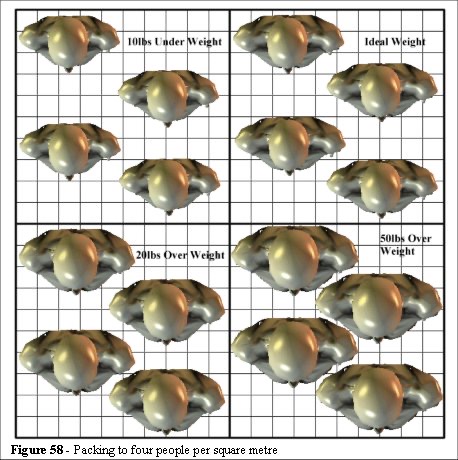
We can see from Figure 58 that packing to four people per square metre, even with a population of very overweight individuals, still allows room for manoeuvre. There is space for the chest cavity to expand, and people have space to move, even if it is only shuffling movement.
The packing density of 4.7 people per square metre with the 50lbs overweight grouping also appears to be within the safety limit stated in the Green Guide. The value of 4.7 people per square metre applies to a stationary crowd [1, 2, 6]. However, as Figure 59 demonstrates, the area per person is not breadth times depth. We shall take the 50cm by 30cm profile, from our discussion in chapter 3.2.2, for our calculations. It represents a significant proportion of the world population in the 95th percentile range of anthropomorphic sizes and falls into a value range which can be handled by the computer, and offers the advantage of being able to use a 10 centimetre scale in the models.

Figure 59 shows that although the body size is 50cm by 30cm, the area that the shape occupies is 929 square centimetres. This would represent a square section of 30.47cm by 30.47cm. Our choice of 50cm by 30cm has the additional advantage for our model; it allows us to use a 10cm resolution as our basic unit of measurement for plans. However, there is a more important reason for using these dimensions.
We know from the Health and Safety Executive experiment in the Taylor reports [32, 33, 34] and observations at Wembley that people can pack to densities approaching 10 people per square metre. We have to allow in this limit on our simulation. If we make the entities too large then the simulation will not allow them to pack to a dangerous capacity and we learn nothing. We would defeat the goal by inadvertently designing a safety margin into our simulation. Our goal is to determine the limits where people can (and will) endanger themselves. The indication is that the simulation has to have the capability of packing to a profile of 30 square centimetres.

We also have to balance the graphical representation with the computational overhead. Figure 60 shows a packing density of 8.4 people per square metre. We can see that at this packing density, we have problems in overlapping complex graphical representations of individual entities. We need to simulate large crowds, greater than 5,000 entities, without incurring a substantial computational overhead.
Complex graphics such as those shown in Figure 60 use a large amount of computer processing. When packing them to realistically high density crowd positions (Figures 9, 10 ,22 34 and 61) we are trying to solve a problem which is know to be intractable; the Knapsack problem. This is a complication we can avoid.

Figures 61 and 62 show moving crowds. At these densities there is room to breathe, space for turning and gaps between individuals. Figures 61 and 62 show that circulation is possible at these densities (estimated at between 4 and 6 people per square metre). Furthermore individuals are not aligned as in Figure 60. This is a problem when we consider the graphics we need to represent entities.
We begin to see the limits to a successful model and the practical issue of the graphics. If we try to make the entities realistic in shape we have a problem working out the high density packing graphics. This is a classing 0-1 Knapsack problem [88] and incurs a considerable computational overhead.
We have to simplify, but not oversimplify, the graphics to make the simulation computationally manageable.

We shall consider a square representation of an entity and discuss the advantages that this presents. Figure 63 shows an entity placed at 0, 45 and 90 degrees on a square grid of 10 centimetre widths. We can see how the 30 centimetre square is a good approximation at all orientations.

Using a square section we can now define two features of our safety limits. The first is that when our simulation exceeds densities above 4.7 people per square metre it is dangerous. The second feature is that we can also time the duration of high density exposure. The square section also simplifies the display graphics yet retains a recognisable form for the individuals.
We can now measure the exposure limit that the entity experiences, giving us a clear indication of his level of distress, and determining the crowd risk factors.
The guidelines use the average density throughout; this is for a very good reason: it has not been possible to analyse the crowd in the above way before. We aim to set new standards in risk and safety analysis for places of public assembly.
5.3 Modelling space
In this section we introduce the concept of information space (iSpace), how it relates to the OMCA rules, and the framework in which we can define complex simulations. First we shall define some of the observations that led to the development of the iSpace concept.
The human body can read and react, at various levels, along the central nervous system. Long before the information reaches the cerebellum the hand reacts to a hot/cold surface. The arm can withdraw (react) to a pain stimulus, effectively bypassing the thought process. This is a fascinating concept in that parts of the central nervous system may be capable of acting without a central processor (the brain). If we adapt this philosophy to our crowd simulation we begin to see how layering sub-programmes, each with autonomous capabilities, can be used to create highly complex behavioural systems. Our model works like the ants in a colony, where a communication system (pheromones) passes information through the colony. Legion entities pass information around the individual entities as the simulation progresses in a similar manner within a framework of logic conditions.
5.3.1 Logic conditions
The rule based system operates with multiple levels of instruction sets. There are three types of logic we use in the model.
- Proximity Logic - Where entities avoid collision
- Conditional Logic - When entities determine objectives
- Absolute Logic - Used to assign structural objectives.
5.3.2 Component definitions
There are two types of components we use in the model. These define the information processing substructure
- Entity - Any component of a system that retains its identity over time.
- Information Space - Any component of a system that has the ability to change over time (in size, internal programming, location). The abbreviation we use for this is iSpace.
Thus an entity contains elements of information and can read and react to the local environment. Communication occurs when entities pass information through the environment. This is equivalent to the ants passing pheromones and building complex interactive communication, and is a decentralised process.
5.3.3 Component communication
The entities contain code segments that interpret iSpace, retain information about objectives, size, velocity and position. Entities’ communicate with (and obtain instructions from) iSpace on a strict hierarchical structure - namely they read the region of that iSpace they are standing on, or are within. That iSpace communication is limited to a single (parent) upper level. The iSpace can then instruct the entity about its objectives.
At each communication stage (a section of the code that searches the entire iSpace structure) the youngest entity (or iSpace component) reads/reacts to the next level up. Once the oldest structure has read/reacted the sequence reverses and works (in a similar manner) from the top down.
Using this method the information is propagated up and down iSpace and all entities/iSpace components are updated (twice per cycle). This structure also allows for a sibling (two components that share the same iSpace) communication as the cycle of upwards communication followed by downward communication relays information across siblings.
5.3.4 Example of iSpace coding
Consider an entity leaving a room in iSpace, where a fire has been lit. Its information from the fire room is leave by any one of the available exits - carrying with it an information segment fire present. It enters the corridor iSpace and is interrogated by that iSpace (which now knows fire is present and where - each entity carries only the flag fire and last destination the code structure on iSpace has an absolute logic map of the environment. This corridor iSpace can now inform every entity within its space of the fire and (as each iSpace module has an objective list) change the probabilities for the next entities’ objectives.
5.3.5 iSpace objectives
It is not necessary for iSpace to have a specific objective (point) as it can communicate an angle to the entity. This can be a collective angle of entities (flocking/migration) or assignment of last entity to next (queuing - also coupled with a speed check - move at the same rate as the entity in front - this then becomes a first in, first out stack for entities). It is also desirable to hold the potential for sorting entity lists in iSpace according to a variety of parameters (such as fuel, cash, size etc.) as conditional logic.
5.3.6 Self-organised environments
Due to the methodology of interactive programming the dynamics of communication is already self-organising. Each entity is dynamically linked to every other relevant entity (via iSpace) and with the hierarchical structure. The structure is constantly communicating across every level. This structure is very similar to that of an ant colony where every ant carries small pieces of information (pheromones) and passes these to others creating a communication system across the whole colony. The collective intelligence of the colony is not in any individual ant, but it exists as a dynamical system protocol. So long as the protocol exists, the colony exists.
In the Hillsborough example we can see that there was no communication between entities, in that the people who were pushing into the tunnel were unaware of those people who were being crushed at the perimeter fence. It is important to note that the collective intelligence of a crowd is, in this way, similar to that of an ant colony. The stadium staff, police and, via the television, millions of people were watching the match, were aware of the event, but the people at the back were not.
When building iSpace we constrain communication between entities in this manner, lest we make our entities too intelligent to place themselves in danger.
5.4 Modelling movement
It is important to define the principles of emergence and how they relate to a simulation. By definition the simulation has to have as few rules as possible to be successful. Those rules also have to represent the characteristics of individuals as they progress through complex geometries, react to differing densities, and act appropriately in a variety of conditions. The conditions can be interpreted by the entities as they navigate the simulation.
To prove the concepts and set a goal or objective for the definition of a simulation, we need to outline the principles we wish to demonstrate. These can be summarised as: To build an entity level model of the hypothetical mechanisms of a behaviour we must:
- Show that, at a fundamental level, the essential elements actually exist.
- Show, by simulation, that the model is capable of generating the observed behaviour (as an emergent phenomenon).
This leads us to the logical conclusion that if the simulation satisfies the process of the behaviour from the proven underlying mechanisms, we have demonstrated the existence of the phenomenon as a well-constructed scientific object.
5.5 Modelling crowds
During the early development of VEgAS and Legion simulation system several hundred hours of video footage, recorded at Wembley Stadium (UK) and a London Underground station, were observed. The qualitative analysis led to some conclusions regarding crowd dynamics which were central to the design of Legion.
Initially the dynamics of how individuals move in a crowd was observed, an algorithm for their behaviour was constructed (VEgAS) and the limitations (computational intractability) for simulation were encountered. A more comprehensive theory was developed and finally the problem of collision detections, culling and real-time analysis were overcome.
The solution to all of the aforementioned problems is encapsulated in the algorithm we call least effort. As mentioned in the introduction the precise contents of this algorithm are subject to non disclosure agreements and commercial constraints. However, we can discuss various aspects of the input parameters and components of the algorithmic solution investigated during the development of the Legion suite of programmes. These include tests on the fingering effect using a random walk algorithm and Monte Carlo models of object navigation.
5.5.1 How people move: a random walk?
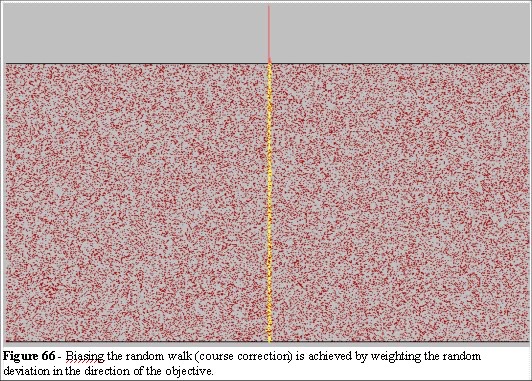
As real people move through their environment they can choose their own direction. We have seen in previous discussions that those choices are influenced by a range of environmental factors. We have also seen that an a priori analysis of all of the choices possible is, by definition, an intractable problem. We have discussed a framework of read and react (iSpace) which allows us to create powerful interactive environments. We have discussed the problems of chaos in computer simulations using the illustration of billiards to discuss the fundamental differences between a physics and biological system with respect to dynamics. First, let us consider a simple model. Figure 65 shows a computer model of randomly located dots on a screen. There is a stream of entities being created at the bottom, and they navigate their way to the top of the screen.
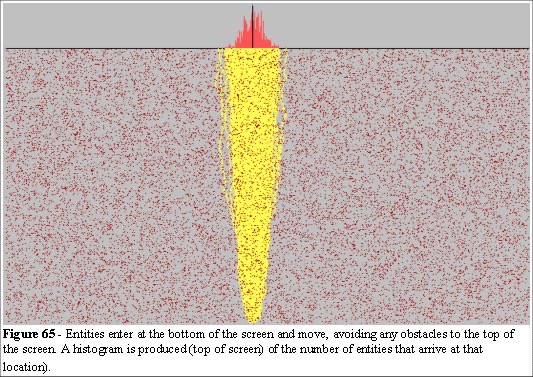
In this model (Figure 65) the choice for avoiding the dots is random. They avoid to the left or right (with equal probabilities) while trying to move up the screen. They keep on their path until another dot (obstacle) is encountered, avoid it again randomly to the left or right and continue until they reach the top. This produces a normal distribution curve of arrivals. The model here is based on the random walk principle and we produce the expected normal distribution curve of arrivals (strictly, a binomial distribution, very close to a normal).
People don’t move like this, the rounding errors in the algorithms have to be compensated for, otherwise the simulation would produce very unrealistic results.
The fundamental differences between a physics model and a biological model is that people can correct their course. The further away they deviate from their shortest route the more they try to compensate.
The field studies observed the degree of noise and course correction associated with the typical walking characteristics of people in crowds. An algorithm that course corrects in the same way that people do when moving through their environment was developed and tested.
5.5.2 Compensating for the random walk.
To ensure these rounding and chaotic errors do not create problems in the simulation we compensate by biasing every deviation choice by the value of the deviation. Thus if the entity starts to drift to the left its next random encounter is biased towards the right.
In Figure 66 we can see the effect of a simple course correction. The point of focus, which we call Objective driven, is compensated as a function of the deviation from the focus. At each stage the entities are reading their current position and reacting to their environment. By using a random function, driven by the deviation from the objective, we can compensate for random perturbations.
We force the system to behave in a more ordered, more biological manner, by this process of course correction.
5.5.3 The rules in a crowd
The simulation uses four rules to determine the functions for the flow of human traffic. These rules interact as characters come into proximity with each others space (iSpace) associated with the static (non movable) and dynamic (movable) objects in the environment. The result exhibits emergent behaviour, specifically, the entities are programmed with one kind of behaviour but the group of entities exhibits another kind of behaviour. Where the group behaviour cannot be reduced to the individuals’ behaviour, a system is defined as emergent.
The iSpace concept allows the design engineer to program emergent behaviour into objects at the object level and construct very complex environments from simple building blocks. This allows them to test complex buildings, part of our objectives outlined in the introduction in chapter 2.
5.6 Intractability of collision detection
Collision detection is a major problem in large scale simulation systems. The main reason why macro-models, based on fluid dynamics, use the Boltzmann Gas equations is that they bypass the problems of collision detection.
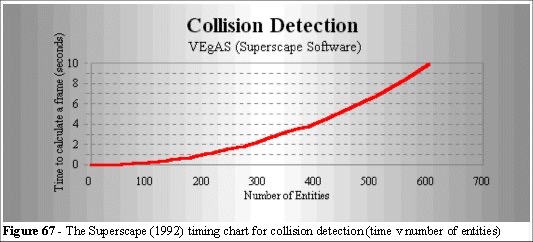
We shall define the problem, highlight its algorithmic complexity, and discuss the solution used in the simulation. First the VEgAS timing chart is presented in Figure 67. The collision detection problem can be tackled by checking each entity against every other entity but that solution is not efficient. As the number of entities increases the time to check through the whole list will rise as the square of the number of objects. Although this is “polynomial time” it is nonetheless computationally intractable in practice for large crowds. The algorithm is O(n2).
5.6.1 Overcoming computational intractability
As the number of the objects rises, the time to check collisions will rise considerably. The VEgAS limitation was a function of the display graphics. Our requirements for a simpler and more relevant graphic in the Legion simulation system. However, we have not yet addressed the problem of collision detection.
If we check from a list of entity positions the system suffers from the problems of computational intractability. The solution was to present the entity with a local environment which can be scanned by that entity.
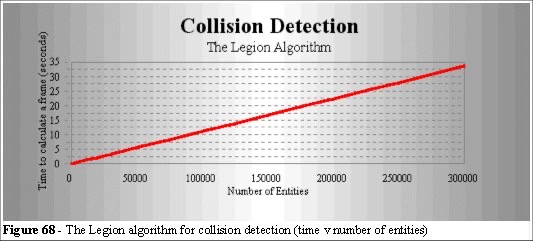
The process we use, described in the introduction, is similar to the approach used for simulated annealing [89]. The least energy constraint has been replaced with a series of least effort constraints. This approach is fundamentally different to the Metropolis algorithm, although in principle the problem is the same. Figure 68 shows the efficiency of the Legion solution. We can see the effectiveness of this algorithm and the results demonstrate that the system performs in polynomial time.
The algorithm does not exceed O(n) time and in areas of high density the algorithm first performs a motility check, then a collision detection.
5.7 The Legion solution
It would be foolish to attempt to construct an algorithm of human behaviour in all its complexity, so we apply Occam’s razor: Our criteria are aimed at safety and risk assessment, the elements that express these parameters are simpler that the complexity of human behaviour per se. Each entity will try to take the shortest route to its objective (fulfilling our least effort hypothesis). They will react to changes around them (this is where we programme the environment in iSpace). They will have no collective intelligence (the exploitation of simple rules is done by many individuals acting independently, they do not perceive the situation as it evolves other than at a local level), they will react to the local geometry by applying simple collision avoidance algorithms, and there is an overall requirement to display self-organisation to the same degree as a high density crowd.
Simple local collision detection scanning has been applied to solve the collision detection intractability. It is simple in concept, but it leads to highly complex results because it has emergent properties.
In a broad description the algorithm scans for the easiest route which is a combination of the shortest distance at the fastest pace. The entities also course correct as they proceed towards their objective. We use the term least effort to describe this algorithm. Strictly speaking the entity is solving a problem know as a nonlinear programme [90]. It does so by taking a least effort route to its destination, working out the shortest distance in two stages: initially calculating a long range scan for the minimum angle navigating obstacles in its way, then scanning for a maximum pace along that route.
We find that the properties we are seeking are incorporated in this simple and elegant methodology. We also find that, when we test the emergent properties, the algorithm is robust and can be validated in a variety of ways against real crowds.
The introduction to chapter 4 listed a series of parameters of crowds, we now examine the performance of the algorithm against those parameters. The crowd consists of many individuals, by design our model consists of many individuals.
5.7.1 Exploiting short cuts
Since we are using an algorithm based on least effort, the exploitation of short cuts is implicit. Furthermore the scan angles we choose are based on the speed of the individual and are adaptive to the local constraints.
It is worth noting that in the Building Research Establishment (BRE) document [29] the following quote appears.
Minor restrictions such as slight projections have little effect on the flow rate. Corners and ends also have no effect on the flow rate. The speed is slowed down and the crowd density is increased on the inside of the bend. On the outside the speed is quickened and the density decreased.
This is due to the people who want to, and are capable of, travelling faster relocating themselves in areas of lesser density. However, the relationship is significant and not, as the BRE document suggests, inconsequential.
5.7.2 Speed profiles in people and crowds
The crowd has a speed profile in that the average speed of the crowd is in fact a distribution of speeds. The crowd can be moving fast at its edges and slow in its middle. The field evidence for this is substantial as we have illustrated in earlier discussion. Edge effects, where the edges of the crowd move faster than the centre, can be observed in many situations. One of the most common places to observe this phenomenon is at a station where people try to get on to a train from a packed platform. We created a simulation to investigate the significance of this effect.
The Edge Effect experiment consists of a corridor with a central constriction: we will call this a bottleneck. The Green Guide suggests that no part of an egress system should be constrained in this manner, and we have seen examples that the Green Guide does not cover (networks and merged flow in particular). In our experiment we consider the space utilisation effect over much larger areas. Specifically we draw on an incident that occurred at Wembley Stadium where the suggestions of the model were implemented (1994).

The merchandising stand (between the trees on the right of Figure 69) was though to be the cause of congestion in this area. Some 20,000 supporters would pass this section. As we can see from the plan (Figure 70) the area has two main directions of ingress flow (shown as blue arrows in Figure 70). The green shapes are concession stands. The red line (Figure 70) indicates the narrowest section on the outer concourse at 18 metres. The problem was related to heavy congestion in this area. The congestion was thought to be attributed to the concession stand on the right; however, the queues to the concessions on the left were actually the problem. The shortest route (Blue arrows) was to cut the corner near the concession stand to the left of the red line above. This clashed with the queue to that concession stand.
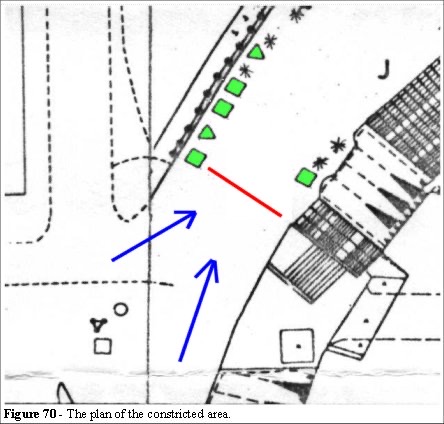
The ensuing flow (left-hand blue line in Figure 70) moved further to the right and the merged flows had higher density (around 5 people per square metre). This resulted in a back-up of supporters, further impeding progress. The problem was solved, not by removing the concession stand on the right (Figure 71) but by removing the concession stand on the left. The queue no longer impeded flow and the congestion was relieved. The density dropped back to 4 people per square metre.
An experiment to test the congestion was created in the simulation tool.
5.7.3 Filling space
As the entity reaches its objective we reduce its speed. Further entities entering that space then have to navigate through the entities already stationary. The result is the same patterns of filling observed in Figures 24 and 71.

Figure 71 demonstrates the principles we need to model in this context.
We can see that people proceed to fill the platform from the bridge (Figure 24), line up along the platform edge. The nearest available space on the edge becomes the next entities objective.
5.7.4 Crowd clustering
We generate each entity at random and assign its speed from the speed distribution histogram. The result is that we can create clusters of slow-moving entities. In tight local geometry we find that the model displays the clusters and bubbles described by Helbing, discussed in chapter 3.5.6. We shall demonstrate the model’s ability to generate clusters and bubbles later in this section.
Clusters occur in two forms: Static and Dynamic; (Figures 72 and 73).

The Static clusters (Figure 72) typically occur in queuing situations. We call this Static because the clusters occur in the same place relative to a location: although the people are moving, the queue remains stationary, that is these types of cluster form standing waves. It is this phenomena that allows us to predict queues (see Queueing Theory).
The Dynamic cluster is observed in areas where packs of high density, slow-moving groups form for two main reasons; small groups can be seen moving together at the pace of the slowest member and the natural occurrence of the speed density clusters, where the movement of people are constrained by a slow-moving individual. These type of clusters form travelling waves.

Figures 72, 73 and 74 illustrate the clustering features. We shall examine these effects in more detail later in chapter 6.4 when we discuss validation of the Legion system. Bubbles of free space in crowds, both stationary and moving, can be observed in Figures 73 and 74. Clusters, small groups of people, are an important feature in the speed/density relationship and we shall examine this in more detail, experimenting with various input parameters. The progress of the crowd is a function of the number of crowd bubbles and clusters. This gives the lie to the assumption that the speed/density relationship is a simple function of density; where density is calculated from the number of people divided by the total available space.
5.7.5 Collective intelligence
Clearly the approach we have chosen has neither collective intelligence, and introduces no a priori assumptions about the collective behaviour of the entities. The crowd may consist of intelligent entities, but their problem-solving skills are not cumulative. Given the circumstances of Hillsborough and other such crowd disasters we can see that the movements of individuals were objective driven. To gain entry at all cost is a necessary criterion for our safety assessment model. If we make any a priori assumptions regarding behaviour we neither discover the potential threats lurking in the geometry nor do we know if our assumptions relating to the crowd speed and density are correct.
Clearly information did not propagate through the crowd at Hillsborough, as people were still trying to gain entry as other died at the perimeter gate. Our model does not need inter-entity communication to evaluate the safety factors. It is far better to approach the problem using dumb entities.
The reaction to the iSpace is not an exception to this rule as we are programming only objective functions within that framework.
5.7.6 Influences of geometry
By allowing each entity to solve their route by applying some least effort criteria, we automatically solve for the effects of local geometry.
If we consider the route that a single entity will take to navigate a corner, we can see that the minimum route assumption appears to be valid. The entity will follow a curve around the corner.
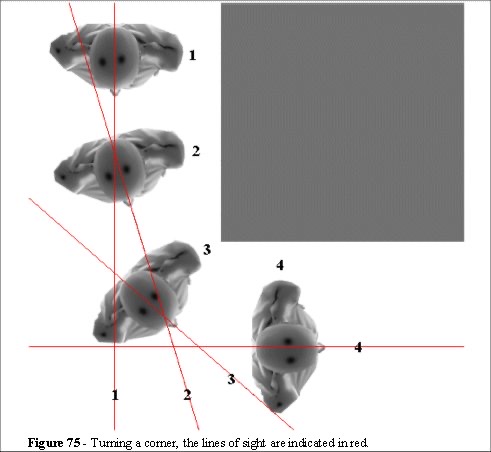
Figure 75 indicates the curve a single entity will take to turn a corner. As it turns its next objective is obscured. It is not until it is in position 3 that it can realign.
5.7.7 Self organisation
The phenomena of bidirectional flow highlighted at the players’ tunnel (Figures 9 and 10), is a self organised characteristic. This phenomenon must arise in the simulation as an emergent phenomenon. It is not a feature that the entities should be programmed to do as that would assume an a priori behaviour that the entities have been told to perform. There are some simple explanations of why it occurs, and we shall demonstrate a model of this phenomenon in chapter 6.
Chapter 2 - Crowd problems and crowd safety
Chapter 4 - Principles of a simulation
Chapter 6 - Validation of a computer model
Chapter 7 - Case study 1: Balham Station